|
|
   |
Homework assignments posted here are subject to correction in class or through other means. Problems as assigned here are for your convenience but are not a substitute for obtaining assignments in class. Assignments as issued in class supersede these assignments unless otherwise noted. Homework Assignment: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Homework #1 (Due January 19, 2010)Modeling and Computing Problems for Class: 1. You will likely use three primary computer based tools during this course. One will be a programming language, such as FORTRAN or Visual Basic. The second will be a CAS, such as Mathcad or Maple. The last will be a spreadsheet. For the program (or language) you expect to use in each of these three categories, you should determine the number of significant digits in the mantissa for a floating point variable and an integer variable. You may express this as a range of base 10 values. Note that in some cases this will involve consulting a manual or help file, but in others may require another approach. 2. Explain why the machine epsilon is often used as a convergence criterion in an iterative calculation, instead of continuing to iterate until the difference in values between successive iterations is zero. 3. Give one example of an engineering problem where each of the following classes of numerical methods can come in handy. If possible, draw from your experience in class and in readings or from any professional experience you have had to date.
Problems for Submission: 4. Examine your engineering textbooks and find four examples where mathematical models are used to describe the behavior of physical systems. List the independent and dependent variables as the parameters and forcing functions. 5. Problem 3.8 in your text 6P (based on 3.3 in your text) Determine the machine epsilon for the computers in the computer lab. You may program in any language that requires you to manually write the code to determine the machine epsilon (you may not use the MATLAB system variable eps, for example). You may use one of the templates available on the course web site for programming in VB or FORTRAN. Download the ZIP file and expand it to a directory called epsilon on your Z: drive. FORTRAN: In your Z:\epsilon\ folder there are several files. Start Compaq Visual Fortran and open the workspace epsilon.dsw in the aforementioned folder. The only source file you need to edit is epsilon.f90. All of the other files, however, are required to generate the working windows program. The comments in epsilon.f90 contain information on the variables already defined for you that you must use for the program to function as intended. You may need to declare other variables in your code. VB: In your Z:\epsilon\ folder is the MachineEpsilon project file. You will edit the Epsilon module. The form and its associated code, including the interface between the form and the global variables is already created. Note the comments in the module file. In either language, you can compile the code without editing anything. The results will be meaningless, but you will be able to see how the finished program will operate. There is very little error checking, so take care to use appropriate input, most importantly keep the stepping factor between 0 and 1. In both cases, submit a printout of your code and a screenshot of the result you obtain. Does the result change if your inputs change? Note that the "proper" way is to start with a value of one with a stepping factor of 0.5.Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #2 (Due January 26, 2010)
Reading Assignments:
Back to Top
Homework #3 (Due February 2, 2010)
Reading Assignments:
Back to Top
Homework #4 (Due February 9, 2010)Beat the System Problem for Class: 1. Chapra 9.11
2.
Cutlip 8.8a, b
3.
The following reactions are proposed to be descriptive of a chemical
process:
1)
CH4
+ CO2
--> 2CO
+ 2H2
2)
CO
+ H2O
--> CO2
+ H2
3)
CH4
+ H2O
--> CO
+ 3H2
4)
CH4
+ 2H2O
--> CO2
+ 4H2
Determine how many of these reactions are independent, and give the equations
for two of the possible independent reactions. Problems for Submission:
4.
Chapra 12.9 (no 4th edition equivalent)
5.
Cutlip 7.14
6.
Cutlip 2.3b,c
7.
Consider heat conduction through the walls of a pipe when the inside wall
temperature is 200oC and the outside wall temperature is 80oC
and the thickness of the wall is 0.05 m.
The inside radius (r0) is 0.05m and the outside radius
is 0.1m.
The differential equation
that describes the temperature distribution is
Applying a finite difference representation of the derivatives of
T with
respect to r gives a set of equations of the following form:
where
and
Solve for the temperature distribution using a Gauss Siedel program you develop
using the Excel/VBA template on the course website. Check your solution by using the matrix inversion
approach in Excel.
Remember that r is not constant. Assignment Learning Objectives:
Reading Assignments: Back to Top
Homework #5 (Due February 28, 2010)An assignment you’ll always regress Problems for Class: 1. 18.1 2. 20.2 3. 20.8 4. Estimate the enthalpy of superheated steam at 741 oF and 400 psia using both linear and quadratic interpolation. Problems for Submission: 5. Using the following finite difference expression for the second derivative: It was found that the error of the approximation was 10-1 using a step size Dx of 10-1. How small should Dx be so that the error of the approximation equals 10-4? 6. A heterogeneous reaction is known to occur at a rate described by the
following Langmuir-Hinshelwood expression: The following data was obtained at 400K:
A) Using multiple linear regression, try to estimate the values of
k1,
KA and
KR 7. Consider the following data on the index of refraction of aqueous solutions of sucrose at 20 oC:
Estimate the composition of a water/sucrose solution which has an index of refraction of 1.3606 by using interpolation and by using regression.
Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #6 (Due March 2, 2010)The integral of the derivative results in this assignment Problems for Class: 1. Using steam table data, estimate the value of the following integral at 700oF for superheated steam using both the trapezoidal method and Simpson’s rule: 2. 23.1 Problems for Submission: 5. 24.6 Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #7 (Due March 9, 2010)Optimize your time as you prepare for the exam Problems for Class:
1.
15.11 2. 16.7
3.
16.12
4.
Find a
journal article referring to the use of a heuristic (random search) optimization
technique in a field related to chemical engineering.
Some algorithms to choose from include: simulated annealing, tabu
search, genetic algorithms, and
neural networks.
Each member of the class should choose a different method.
I suggest you limit yourself to journals obtainable online.
In class, you will be expected to briefly explain the method and its
application in a presentation to last no longer than 5 minutes.
Any images you wish to use should be submitted to me electronically at
least 1 hour before class. Problems for Submission: 5. 13.11 6. 16.6 7. 16.10
8.
You are required to produce an alloy that has at least 30% Pb and at
least 30% Zn by mixing a number of available Pb-Zn-Sn alloys.
Find the cheapest blend using the method of Lagrange Multipliers.
9.
Submit the complete text of the journal
article (from problem 4), along with a summary (<1 page) indicating how the
technique was used.
You should also
include comments on why this method was chosen by the author and provide a brief
description of the method. Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #8 (Due March 25, 2010)Returning to Where the Fun Began Problems for Class: 1. Problem 11.4 from Felder/Rousseau (FR) Problems for Submission: 3. Problem 11.16 (FR) Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #9 (Due April 1, 2010)Don’t be overanalyticalIn addition to the instructions for each problem, you should also:
Problems for Class: 1. Desalinization plants are used to purify sea water so it is suitable for drinking. Sea water containing 8 g salt/kg solution is pumped into a well-mixed tank at a rate of 10 kg/min. Assume that the balance of the solution is pure water. Because of faulty design work, water is evaporating from the tank at a rate of 0.5 kg/min. The salt solution leaves the tank at a rate of 10 kg/min. A) If the tank is filled initially with 1000 kg of the inlet solution, how long after the outlet pump is turned on will the tank run dry? B) Determine the salt concentration in the tank as a function of time. Problems for Submission: 2. A spherical ice cube (an "ice sphere") that is 5 cm in diameter is removed from a 0 °C freezer and placed on a mesh screen at room temperature Ta=20 °C. What will be the diameter of the ice cube as a function of time out of the freezer (assuming that all the water that has melted immediately drips through the screen)?3. Compound
A diffuses through a 4-cm-long tube and reacts as it
diffuses. The equation governing diffusion with reaction is
Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #10 (Due April 13, 2010)Everything Changes With Time Problems for Class: 1. 25.1 Problems for Submission: 5. 10.2 from Cutlip 6. Consider the semibatch reactor discussed in class, now with the following reaction scheme:
Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #11 (Due April 22, 2010)Oodles of ODEs Problems for Submission: Problem for Class:1. Chapra Problem 28.10 solved using a computer program of your choice. Problems for Submission: 2. Consider the cooling fin pictured below. 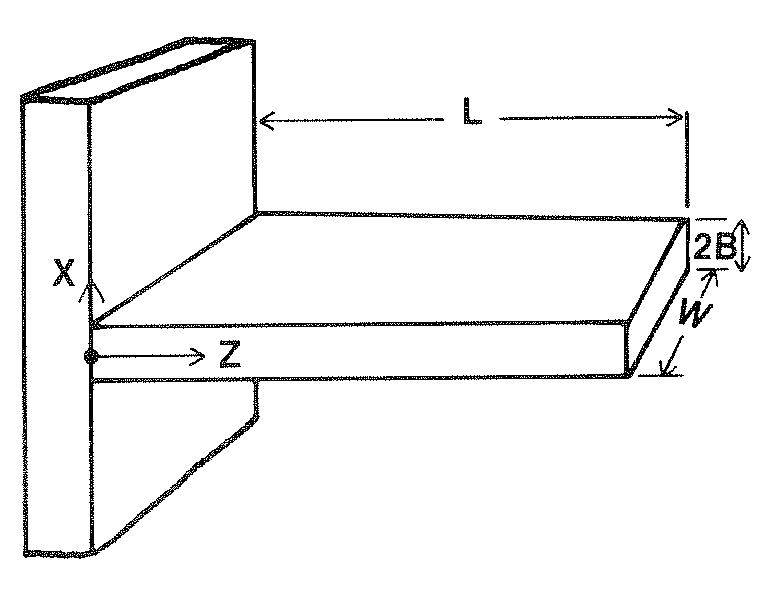
A shell balance results in the following energy balance expression
where T =Tw at
z = 0 and
A) Consider the temperature dependent of k and show that the governing equation for this system is
B) Solve this problem to three significant figures in T using the SOR method and the following values: h0 = 40 Btu/hr-ft2-oF k0 = 60 Btu/hr-ft-oF a = 0.02 oF-1Tw = 450 oF T0 = 77 oF Ta = 90 oF L = 1.5 in B = 0.02 in 3. Cutlip Problem Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #12 (Due April 29, 2010)You Can Simulate This If Needed Problems for Submission: 1. Problem 10.13 from Felder-Rousseau (FR). 2. Develop a simulation in Aspen for the same scenario in 10.13a. Compare results with your spreadsheet and hand calculations. Why the differences? Correct for those differences in your Aspen simulation wherever possible. Assignment Learning Objectives:
Reading Assignments:
Back to Top
Homework #13 (Due April 21, 2004)Back to Top
Homework #14 (Due April 30, 2004)Back to Top
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Access to material copyrighted by anyone other than the instructor is restricted
to students enrolled in this class at the University of Kentucky Extended Campus
at Paducah. Questions or problems regarding this web site should be directed to Dr. Silverstein. Copyright © 2005-2010 by David L. Silverstein. All rights reserved. Last modified: Monday April 19, 2010. |